
The graph of the right-hand side of \(x^5 = −32\) is a horizontal line, located 32 units below the x -axis. The graph of the left-hand side of \(x^5 = −32\) is the quintic polynomial pictured in Figure 4. This is pronounced “the negative fourth root of 16 is −2.” A negative exponent means how many times to divide by the number. Multiplication is commutative, so when multiplying numbers in scientific notation multiply the. Choose to place the decimal so that the first digit is between 1 and 10. Express the number in scientific notation. Obtain the same result by moving the decimal over to the left 4 places.
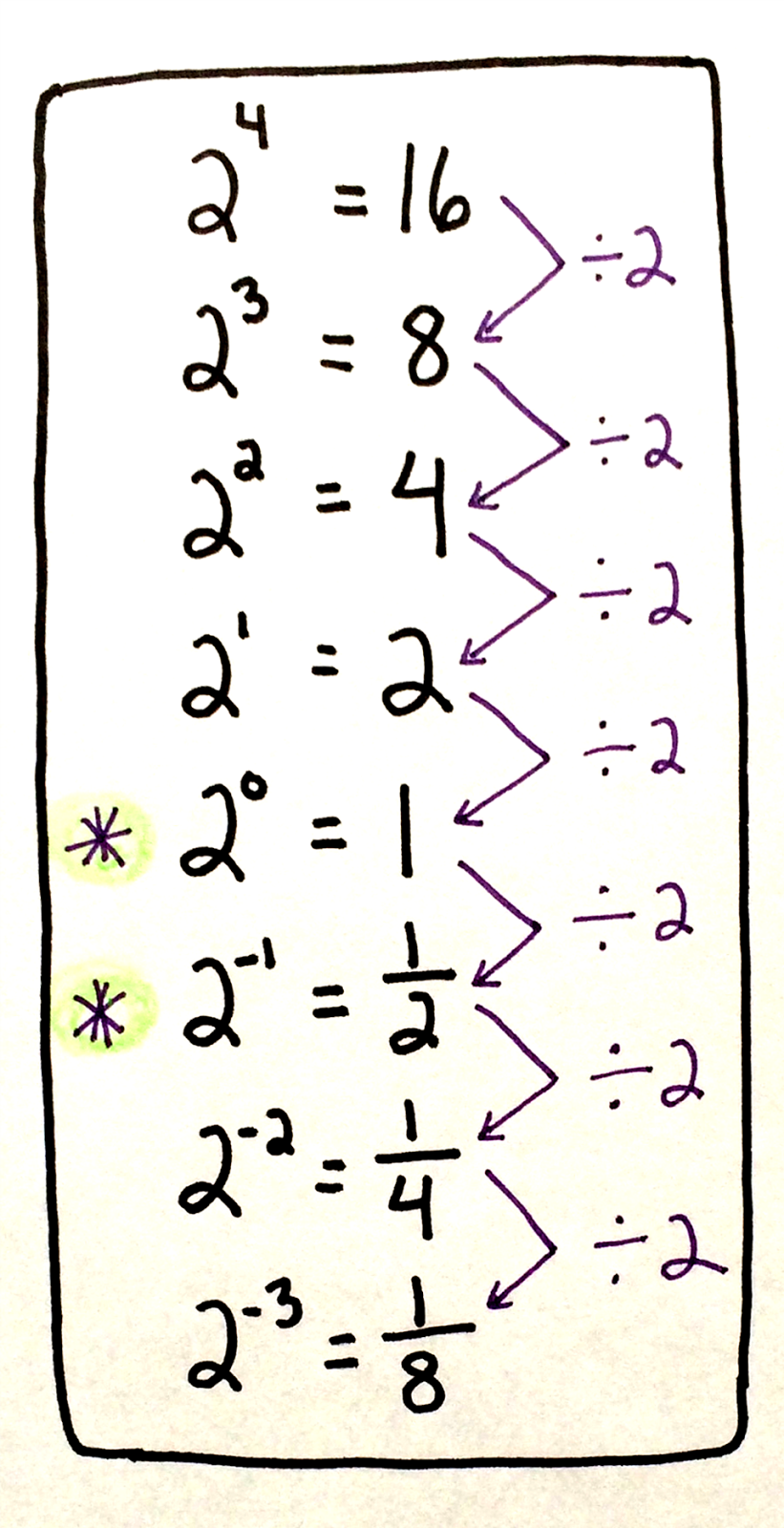
For this negative solution, we use the notation Negative exponents appear when working with very small numbers. On the other hand, note that \((−2)^4 = 16\), so x = −2 is the negative real solution of \(x^4 = 16\). This is pronounced “the positive fourth root of 16 is 2.” A factor with a negative exponent becomes the same factor. For this positive solution, we use the notation This is true for any nonzero real number, or any variable representing a nonzero real number. Why can't a monomial have a negative exponent What does the power rule for exponents states Justify along with an example.

Explain why polynomials can't have negative exponents. Why/how does the exponent of 1/2 mean the square root Explain. Note that \(2^4 = 16\), so x = 2 is the positive real solution of \(x^4 = 16\). Why can't polynomials have negative exponents Explain three rules of exponents giving examples in each. There are two basic rules related to negative integers with exponents: If a negative integer has an even number in the exponent, then the final product will always be a positive integer.

Hence, we need two notations, one for the positive fourth root of 16 and one for the negative fourth root of 16. It is extremely important to note the symmetry in Figure 3(c) and note that we have two real solutions of \(x^4 = 16\), one of which is negative and the other positive.


 0 kommentar(er)
0 kommentar(er)
